Class Registration Banner" width="768" height="128" /> Class Registration Banner" width="768" height="128" />
We are familiar with the terms Domain of a Function and Range of a Function. But what does it mean? Before diving deeper into the topic, let us understand what a function is? Then, get into the detailed explanation of the domain, range and codomain of a function, along with solved examples.
Functions are one of the fundamental concepts in mathematics which have got numerous applications in the real world. Be it the mega skyscrapers or super-fast cars, their modelling requires methodical application of functions. Almost all real-world problems are formulated, interpreted, and solved using functions.
An understanding of relations is required to learn functions, Knowledge of Cartesian products is also required to learn about relations in maths. A Cartesian product of two sets A and B is the collection of all the ordered pairs (a, b) such that a ∈ A and b ∈ B.
A relation is a subset of a Cartesian product. Thus, a relation is a rule that “relates” an element from one set to another. A function is a special kind of relation. Let’s consider a relation F from A set A to B
Definition: A relation F is said to be a function if each element in set A is associated with exactly one element in set B.
To understand the difference between relations and functions with the help of an example.
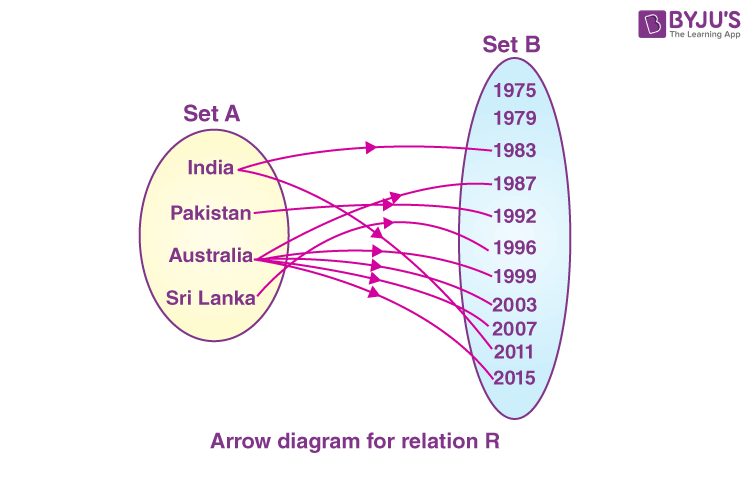
Set A = Names of all countries that won the cricket world cup
Set B = List of years in which the world cup played
The arrow diagram shows (in the figure below) the relation R but not a function.
This is because elements of set A are associated with more than one element of set B.
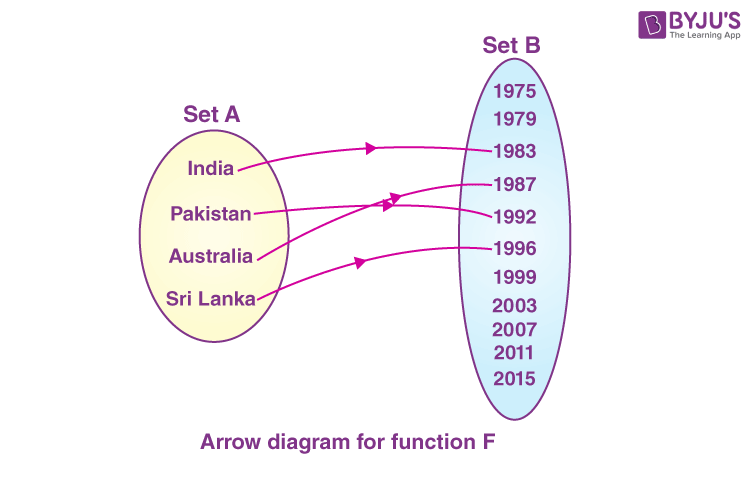
Suppose we define a relation F from set A to B such that it associates the countries with the year in which they won the world cup for the first time. Thus, every element in set A will be exactly associated with only one element in set B.
This relation F shown in the below figure is qualified to be a function.
Remember that in the case of a relation, the domain might not be the same as the left set in the arrow diagram. This is because the set may contain any element which doesn’t have an image in the right set. But in the case of functions, the domain will always be equal to the first set. Range and Codomain of a function are defined in the same way as they are defined for relations.
The domain and range of a function can be identified based on the possibility of the given function to be defined in the real set. Let’s have a look at Domain and Range that is given in detail here.
The set of all possible values which qualify as inputs to a function is known as the domain of the function, or it can also be defined as the entire set of values possible for independent variables. The domain can be found in – the denominator of the fraction is not equal to zero and the digit under the square root bracket is positive. (In the case of a function with fraction values).
For e.g. the domain of the function F is set A i.e. .
The set of all the outputs of a function is known as the range of the function or after substituting the domain, the entire set of all values possible as outcomes of the dependent variable.
For e.g. the range of the function F is . On the other hand, the whole set B is known as the codomain of the function. It is the set that contains all the outputs of the function. So, the set of real numbers is a codomain for every real-valued function. The codomain of the function F is set B .
